Today your mission is…

Play the multiplication model bingo to see a variety of models wherever you go.

Ready, Set, Go

This is the same scavenger hunt you did during Week 1 task, What Is Multiplication. This time, invite your kids to hunt with you. Many people say they get stuck seeing the same model everywhere. Can you find all 12 models? You can print out this bingo sheet with spaces for your finds.

Your forum response

• What multiplication ideas do you see in this topic? What bridges connect this to your everyday life, sciences, and arts?
• Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?

How to help your child to get started

This activity is sort of like a scavenger hunt, only you are allowed to create your own models.

You might end up being the first who notices a particular model. Point it out to your child and connect it to an activity you did in the previous weeks. If you are stuck looking for a particular model, go through the artwork and other artifacts you and the children created over the last couple of weeks.

Find different examples of the same model. Help kids point three tips of a leaf with three fingers, hold the puppy four paws up, put feet on the two levels of a climbing structure and otherwise show numbers with bodies, as you take photos. If your child really likes a find, reproduce it in LEGO, playdough, Minecraft, paper, etc.

Frequently Asked Question

When I do these activities with my child, I feel like I need to actively teach - talk about what goes on and why. I think I’m doing too much of it though, taking over my child’s math exploration. What should I do?

You can lecture occasionally - when your child asks for an explanation. Keep it under a couple of minutes. What to do during the rest of the time? Be active, yes, but in a variety of ways: as a coworker, a naturalist-researcher, and a guru. As your child’s coworker, play in parallel: do your own experiments and explorations of the same math your child is exploring, because it creates a smooth workflow and inspires ideas. As a researcher, observe the elusive natural behaviors of your kid, take notes and photos, gently ask non-leading questions, because it will help you preserve your child’s well-being, and nurture a healthy ecology of learning. As a guru, your goal is to help kids be heroes of their own adventures. Play Yoda to your kid’s Luke.

Bob Kaplan, a math circle leader and author, says the trick is to become invisible. Active, but invisible! Read more here - http://www.moebiusnoodles.com/2013/09/becoming-invisible/

Words

Array, area, number line, set, combinations, symmetry, fractal, scale

Today your mission is…

Fill times tables with personally meaningful examples. This task helps to develop fluency and applications of multiplication.

Ready, Set, Go

This activity scales up and down: you can spend five minutes, or five hours, or five years hunting for the elusive facts. Don’t worry about finishing it all in a day. Just as with any other collections, this one will grow and become more meaningful over time.

Go on a scavenger hunt for examples of multiplication in nature, designs, or stories. Prepare index cards or sticky notes, and a times table grid large enough to fit them. Every time you find an example, sketch or describe it, and put it in the right cell. Some combinations are easier to find than others, so you can have multiple cards in the same cell. Decide what to do about the symmetric times facts, like 2*5 and 5*2. Take photos of happy hunters with their finds and creations!

For an extra challenge, seek iconic examples, where objects always go with particular numbers. Hands and fingers always mean 2x5, and the chessboard is always 8x8.

If you are into arts, crafts, or engineering, make your collection beautiful. Go from a sketch to a full art piece. Compose your photos nicely. Design a complex Lego sculpture or Minecraft building. Turn a description of a situation into an engaging story. Make a poster, a collage, a gallery, or a diorama out of your collection.

By Sabdha C.

Your forum response

• What multiplication ideas do you see in this topic? What bridges connect this to your everyday life, sciences, and arts?
• Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?

How to help your child to get started

Where can you go hunting?

• On a field trip. Your yard, a park, a museum, a fire station, a zoo… Give each group of participants a camera to capture their finds. Invite them to point out multipliers they find with their hands or whole bodies for extra awesome photos.
• To your home. Find multiplication in toys, pets, decorations, books. Make mobiles or sculptures about multiplication.
• To a virtual world. Find and build multiplication in the universes people created, such as Minecraft, Star Wars, Dungeons and Dragons, and Harry Potter. Let kids pick destinations.
• To a box of construction toys and art materials. How many different ways can you show the same multiplication example with Legos? Can you paint it, sculpt it, fold it, cut it?
• Through history and ethnography. Check out what different times and cultures did for their multiplication, from playing dice to building abacuses.
• Into a trade. How do nurses, astronauts, musicians, or homesteaders use multiplication? You can interview a real tradesperson, or pretend-play about sci-fi, historical, or future professions, such as alchemists, Mars settlers, or time travelers.
• Into the imagination. Make up stories and art devoted to multiplication. Play “Imagine That!” by making silly changes to the world: a hand with fingers at the tips of fingers, a dog with eight legs, an alien planet where numbers only went up to three.

Frequently Asked Question

You frequently mention celebrating mistakes. But how to do it? And why? In life, making a mistake may lead to unfortunate or tragic consequences. Does celebrating mistakes mess up children’s respect for serious thinkers of the past?

You would not celebrate a mistake in building a bridge, or in getting the distance to Mars wrong and missing your landing window! However, there is a side of mathematics that is more whimsical and free. Mathematics can be not only about measuring this world where we live, but about making up other, fantastic worlds. In that, mathematics is closer to fairy tales, or science fiction, or fine arts where you can create rather freely. So when I talk about celebrating mistakes, I mean taking them from our world into one of those mathematical Wonderlands.

For example, my math circle kids kept confusing squares and cubes, or circles and spheres. But we played with it, and by now, they talk about three-dimensional squares - or even four- and five-dimensional! This road from mistakes to abstractions is a big part of the history of serious mathematics, from imaginary numbers to non-Euclidian geometries.

Words

Array, area, number line, set, combinations, symmetry, fractal, scale

Today your mission is…

Build decanomial squares, using the array model of multiplication. Array is the best model to explore algebraic properties of multiplication such as commutativity, and algebraic identities such as (a+b)^2=a^2+2ab+b^2

Ready, Set, Go

A decanomial square is a multiplication table made out of arrays. You can use different materials to build your squares.

Graph paper, by Somewhat in the Air. You can design and print graph paper online or make it by hand. Use larger cells with younger kids.

Homemade Montessori beads, by Our Homeschool Journey. This takes a long time to make by hand!

Felt, by Walk Beside Me. Note that unmarked pieces have more perplexity, forming visual, geometric puzzles. Bead pieces or graph paper pieces are easier to sort and push toward number patterns and algebra. You can make the same design out of construction paper.

Cuisenaire rods, by Simon Gregg. This combines visual aspects (rods don’t have unit marks) with counting (the number of rods).

Your forum response

• What multiplication ideas do you see in this topic? What bridges connect this to your everyday life, sciences, and arts?
• Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?

How to help your child to get started

Reach for your child’s favorite medium whether it’s clay, paper, beads or anything else. Start the pattern and ask the child for help. Play “what goes next” game. Make mistakes in the pattern to give your child an opportunity to correct you.

If you are working with younger children, keep the squares small, only two (binomial) or three (trinomial) numbers. The squares can grow with your child.

Photo of trinomial square and cube by Simanaitis Says

Frequently Asked Question

When it comes to “continue the pattern” activities, my child is quick to figure out the pattern, but starts making mistakes after just a couple of steps. Why? How can I gently correct my child’s mistakes? And should I do it in the first place?

For the reasons why kids break patterns, revisit our activity Your Child, the Divergent Thinking Genius. Consciously or not, children play around, change patterns, notice and immediately implement new possibilities. An adult is likely to hold a neat alternative for later, while carrying on the current pattern. Many kids don’t see any point in carrying a pattern beyond the moment they understood it.

Once a kid gets a bright new idea, it’s very hard to carry on the old pattern, even if the kid wishes to do so (which is rare). Children don’t have enough short-term memory or attention to hold two patterns in mind. So for children, the healthy way is to implement their bright ideas right away, lest they forget!

Don’t think of pattern-breaking as a mistake, because most often it isn’t. It’s play or creativity. Don’t: distract the child from brainstorming about patterns! Let the child play. Do:

1. Observe quietly for a while, to understand (or to make up) a pattern behind your child’s new idea.
2. Copy that new pattern yourself, making 4-5 steps of it. When your child pauses from play, ask if you got the idea right.
3. Sometimes children keep changing the rules again and again. Make all the patterns you notice.
4. Also make the old, original pattern. Admire, compare, and photograph all the patterns you made together.

Think of yourself as a catcher of the wild patterns your child generates. Gotta catch them all!

Words

Decanomial, commutativity, square, binomial, trinomial

Today your mission is…

Find and color-code patterns in the times table. If you look at the times table long enough, algebra will look back at you. Instead of 100 (or 144) disjointed facts, you’ll see a jigsaw of clear, orderly, beautiful patterns. The mastery of patterns is required to be a mathematician, a scientist, an artist, or an engineer.

Ready, Set, Go

Some kids like to memorize number patterns. Others do so because of requirements. Others keep a pocket times table with them, or use calculators. This activity is designed to help all these kids, in different ways.

Invite your kids to look at the times table and color any sequence or pattern they notice. It might make sense for adults to describe such a pattern as, “A group of facts you know without any need to memorize.” Younger kids may not understand what “need to memorize” means, but they can still seek patterns. For example, there is the counting sequence 1, 2, 3 in the table; the counting sequence with zeroes behind the numbers (times ten); and the doubles, which many kids find easy, especially after activities from the past weeks. There are more exotic and hidden patterns for those who like number play. Keep seeking!

Your forum response

• What multiplication ideas do you see in this topic? What bridges connect this to your everyday life, sciences, and arts?
• Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?

How to help your child to get started

It is not necessary to reduce the table to something smaller if you work with young kids. After all, seeing more examples might help them notice the patterns. However, you do need larger cells, with numbers in large font. For toddlers and young kids who don’t yet know or are not fluent at recognizing numbers, this dot version will work. You can make your own posters using factorization diagrams.

Adapted from factorization diagrams at Math in Your Feet, Nike Naylor, and DataPointed.

It may help you to know, ahead of time, what types of patterns other people have found in the times tables so far. This does not mean you need to guide your kid to find all these patterns - let alone on the first day! This is to prepare you to expect the unexpected, because patterns come in many types. For each pattern, investigate why it works.

Patterns by the skip provide a sequence of skips that is easy on the eye.

• *10 all end in 0s: 10, 20, 30, 40…
• *2 are even numbers: 2, 4, 6, 8...
• *5 end in 5s and 0s by turn: 5, 10, 15, 20…
• *1 are counting numbers: 1, 2, 3, 4…
• *11 have repeating digits: 11, 22, 33, 44...

Personal patterns are sequences or individual facts you love and remember, for reasons of your own.

• People who like geometry love square numbers that sit on one diagonal of the times table: 1, 4, 9, 16…
• Poets love and remember rhyming or alliterating facts: six times six is thirty-six; five, six, seven, eight - fifty-six is seven times eight; five times five is twenty-five, etc.
• Psychologists note 7*8, 6*9, 7*9, and 6*8 as the facts that cause people the most confusion (see Dehaene, “The Number Sense” chapter “The multiplication table: An unnatural practice?”)
• Western musicians pay a lot of attention to *4, because many songs are in measures of four.

The symmetry pattern means that 2*5 is the same as 5*2. It makes the top right and bottom left corners of the table hold the same exact numbers, as if the diagonal were the mirror. Some people call this the commutativity pattern after the name of the property. Toddlers and young kids often like pretty math terms like this! For anyone who memorizes facts, this pattern reduces the workload almost in half.

In the nines pattern, there are many ways you can notice regularities.

• The first digit is increasing by one and the second digit is decreasing by one: 09, 18, 27, 36…
• Times nines are 1, 2, 3… away from the corresponding times tens: 09 and 10 (1 away), 18 and 20 (2 away), 27 and 30 (3 away) and so on.
• Spread your ten fingers and fold away the Nth from the left. You will see the answer to 9*N in the remaining fingers. Here’s a video from PBS: https://www.youtube.com/watch?v=Wu3JSnRaaV0
• The sum of the digits in the times nine results (up to 90) is always nine. The first digit is one less than the number you multiply by nine.

Calculation patterns are for people who love number crunching or number puzzles.

• Off-diagonal numbers run parallel to the square diagonal. They are facts like 4*6, 7*9, and in general (N-1)*(N+1). They are one less than square numbers.
• You can find a similar off-off-diagonal pattern for (N-2)(N+2), and so on.
• Times 4 is doubling, twice.
• Times 8 is doubling, thrice.
• A finger reckoning trick from 15th-century merchants, now a fun parlor trick, shows how to multiply numbers 6-9 on your hands. See details here: http://www.moebiusnoodles.com/2014/04/multiplication-a-parlor-finger-trick/

Frequently Asked Questions

Parent 1: My child believes that he is not good at math. In fact, his conceptual understanding is strong, but he’s a bit slow on calculations. Any time I suggest we play a math game or do a math activity, he just shuts down if he suspects it involves calculations. I don’t want to force him, but I do want him to be braver, and to learn how to calculate.

Parent 2: My child is overly confident, I think. Five minutes into a new activity he proclaims he’s good at it, so he’s done. He doesn’t stop to check if his answers make sense, such as 5000 mph car speed. I don’t want to lessen his confidence in himself, but I do want him to check his work, and not to be arrogant.

The two very different stories reflect the same key difference between kids and adults: metacognition, or knowing about knowing. Parent 1 and Parent 2, it’s frustrating that your kids don’t know what they know, but the good news is this is unlikely to be about character flaws of timidness and arrogance.

Use math tools to help kids grow their metacognitive skills, such as:

• Know what to check when you solve problems, where you are prone to mistakes (such as forgetting to check if 5000 mph is realistic for cars).
• Use your strengths to your advantage, pick tasks that match your strengths (Child 1 is beginning to get this awareness).
• Know your weaknesses and how to compensate for them; seek techniques, tools, learning, and helpers that can cover you (for example, using key terms from a text to seek images, if you don’t learn well from texts).
• Be aware of math values such as precision and rigor, and your personal math value system (for example, little engineers say you can’t really split a fractal into parts infinitely many times, because you have to stop at atom size, since they value realism).
• Know the size of your working memory; optimize your use of working, short-term, and long-term memory for your tasks (for example, use the partial quotient long division algorithm, which is less taxing on working memory).

Some people believe metacognitive skills can’t develop until adolescence, but we don’t think so. You can and should develop healthy math habits early on. This includes children appreciating some psychology of learning mathematics. For example, check answers after each and every problem, at all times, as a habit - but discuss how best to check for each problem. Play memory games and solve the same memory-intensive math exercises during different times of the day, so you can compare and discuss differences in how your mind works. Try to present the same problem as a picture, text, hands-on model, or whole body experience, and see which way makes sense. It will vary by problem, but some people do have favorite learning styles. In short, learn about mathematical metacognition yourself, and help your kids know what they know. Some resources to get you started:

• The Brilliant Blog
• Math Mind Hacks
• How to solve it (awareness in problem-solving)

Words

Pattern, formula, rule

- Why are waiters good at multiplication?

- Because they know their tables!

Today your mission is…

Learn the spaced repetition method for memorizing bodies of facts.

We memorize times tables to

1. Have an easy, reliable, quick access to each individual fact.
2. Notice and use more number patterns.

Notice that we say access, not recall. Most people don’t memorize facts like 2*2, 1*7, or 10*9, because they can calculate the answers very easily.

Strongly visual people often close their eyes to access facts (to imagine some pictures), auditory people mutter, and kinesthetic people move their fingers. These techniques aid either memory or calculation, and should be encouraged.

Quiz before you start

Which of the following methods of memorizing serve Goal 1, 2, or both? Answers with comments are at the end.

1. Memorizing by reciting whole times tables in order (*2, *3, *4…)
2. Memorizing by reciting times tables (*2, *3, *4…) plus training access to individual facts out of order.
3. Memorizing multiplication songs.
4. Using pictures and stories with mnemonic clues for the multiplication facts.
5. Memorizing by patterns.
6. Memorizing by patterns plus training access to individual facts out of a pattern.

Ready, Set, Go

This activity is for people who consider memorizing multiplication facts. We do not have enough data to tell you whether memorizing times tables is a good idea, mathematically speaking. But many people will like this as a mental exercise, just as people enjoy memorizing music and poetry. Many will find it useful for social reasons. We recommend memorizing by patterns plus training facts out of order.

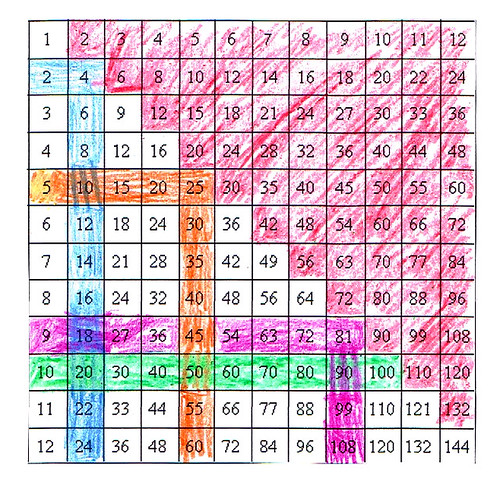
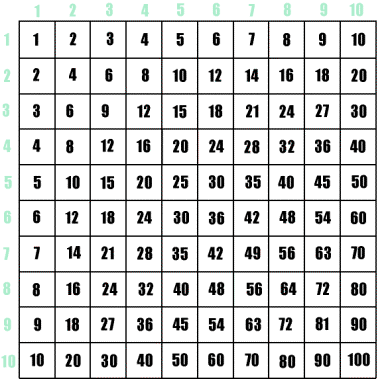
First, do the triage of patterns from the activity Coloring the Table. Which patterns do you know well enough that you don’t need to memorize? Throw these facts out of your table! Cross them out. Different people make different decisions. We strongly recommend getting rid of ones, tens, and the symmetry (commutativity) pattern, leaving you with this:

You are down to 36 facts from 100, without doing any memorization! You may cross out even more patterns, for example, many people remove times two. Also cross out individual facts you happen to know. Now pick a pattern from the list of what is left, and use the spaced repetition method on these facts.

Option 1: Paper cards

Preparation

1. Make cards for each fact from one pattern. Write the multiplication (such as 3*9) on one side of the card and the answer (27) on the other side.
2. Cross these facts out in the table to mark your progress.
3. Make three boxes for the cards: Easy, Good, and Again. Place all your cards in the Again box for now, multiplication side up.

Work with your Again box two times a day

1. Take the stack from the Again box, shuffle it, and try to access each answer in your mind. Then turn the card over to check yourself.
2. If you accessed the fact as fast as you want, and correctly, move it to the Easy box. If you accessed the fact a bit too slowly but correctly, move it to the Good box.
3. If you could not access the fact, were very slow, or made a mistake, do a micro-exercise for your memory. Say the fact out loud: “Three times nine is twenty-seven” and/or imagine any visuals that go with that pattern, such as a three by ten array with the top three counters crossed out. Put the card back into the Again box.
4. If your Again box is empty, congratulation! You made great progress on that pattern. Refill the Again box with new cards, from the next pattern you want to tackle.

Work with your Good box once a day, and with your Easy box once a week. Occasionally, you may need to move a card back from Easy to Good, or from Good to Again - that’s fine, don’t worry. Eventually, all cards will migrate to Easy. Workouts should be under two minutes.

Option 2: Memory software

We highly recommend the free software Anki. You can make a deck of Anki cards for each pattern. The software will keep track of which card to use, and how often. In the long run, it is much easier to use and more efficient than paper cards. You can use the same tool for learning foreign words, scientific terms, flags of the world, and other bodies of facts.

As an example, you can download MariaD’s deck of some squares.

Your forum response

• What multiplication ideas do you see in this topic? What bridges connect this to your everyday life, sciences, and arts?
• Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?

How to help your child to get started

Help your kid make all the choices about the process. When during the day is it better to do this work? Which patterns to train, and which not to train? Which pattern comes next? If you work with paper cards, help to make the cards and their boxes beautiful. But don’t decorate cards with stickers or extra pictures, because that will mess up your memory. You can decorate the boxes.

Frequently Asked Question

I thought there were no pre-requisites for the activities in this course. Doesn’t my child need to know numbers first?

With children who do not yet know number symbols, use dots arranged in meaningful patterns, or objects that show quantities. Say the description out loud. Only use two or three cards or toys at one setting, unless your kid insists on more. Make it possible to answer with pointing or picking the right object, rather than words.

Here are some good patterns to use with toddlers:

• Dice and playing cards
• Montessori beads, Dienes blocks, algebra tiles
• Triangular, square, and other shape numbers
• Animal legs or other iconic quantities

Words

Recall, fluency, access, pattern

Quiz discussion

Goals:

1. Easy, reliable, quick access to each individual fact.
2. Noticing and using more number patterns.

Only two methods serve both goals. Of these, #2 (Memorizing by reciting times tables (*2, *3, *4…) plus training access to individual facts out of order) takes longer, is less engaging, and will serve the second goal less than #6 (Memorizing by patterns plus training access to individual facts out of pattern). We recommend that method, #6.

If you do #2 (Memorizing by reciting whole times tables in order (*2, *3, *4…)) or #5 (Memorizing by patterns), Goal 1 is at risk, because you have to access the whole list or pattern.

More dangerous are #3 (Memorizing songs) and #4 (Using pictures and stories with mnemonic clues for the multiplication facts), and other non-mathematical mnemonics. They can jeopardize you seeing mathematical patterns, thus your understanding of algebra. Though songs are less dangerous, since people are less likely to overuse them.

Hi I’m Rachel. I’m a high school student. I need your help with a book I’m co-authoring.

Imagine you are sitting in math class. The room is stiflingly hot. Your teacher is droning on and on about factoring, something you really couldn’t care less about. The kids next to you are passing notes, quietly murmuring. A stifled burst of laughter. Your eyes start to droop. Your desk is such a comfy pillow. You’ll just close your eyes for a few minutes, and then you’ll pay attention. Just a few minutes…

It’s a classic problem. Let’s face it, everyone gets bored sometimes. What should students do when they get totally bored in math class?

Lots of people have invented different coping strategies. When Vi Hart is bored, she doodles. When Trachtenberg was bored, he mentally manipulated numbers. The Happiness Project says to notice your surroundings, or to just plain keep trying. In internment camp, Pilates invented, well, Pilates. When Gauss was given boring math exercises to do, he invented an algorithm to make them go faster so he could do something interesting. What should you do when you’re bored in math class?

I’m collecting input for my book and I want your ideas. Please reply with them. Thank you so much!

Posting for a young friend - MariaD

Camp Logic is a book for teachers, parents, math circle leaders, and anyone who nurtures the intellectual development of children. It is not necessary to have any mathematical background at all to use these activities – only to have a willingness to dig in and work toward solving problems where there is no clear path to a solution.

You can help us publish Camp Logic! Let your friends, colleagues, and the world know you want children to enjoy the underlying structures of math: share the crowdfunding page on your sites, blogs, and social media. Join the crowdfunding event to contribute money for editing, printing, and distributing the book, and to field test the activities. The book will by published in 2014, under an open Creative Commons license.

-- Mark Saul and Sian Zelbo, authors

The campaign reached its first milestone, so we are opening the draft of the first chapter for everyone's preview and discussion. It is attached to this post. Answer to share your thoughts, feedback, and questions for Mark and Sian!

Camp Logic Day One PDF

Please note that we will do layout (such as splitting into pages) and copy editing (for typos) later, after we incorporate reader comments. Now you get to see how a draft looks before the book is laid out!

Here are a few questions to get your feedback started!

• How good was the chapter overall? What caught your eye?
• Were there parts where you wished for more details?
• Were there confusing parts, problems you did not know how to start, or other roadblocks?
• Have you noticed anything we need to fix about spelling, grammar, and style? Any other comments to the editors?
• What do you think of illustrations?
• Do you feel you could run these activities with kids after reading? If not, what other support would you need?
What do you think of this chapter? Do you have questions, comments, any feedback to the authors? Reply below!

If you are reading this, you should have received five chapters of the Camp Logic book by email. Please answer some of these questions, leave other feedback, or ask questions. Any feedback will help Mark Saul and Sian Zelbo to improve the book. They will reply to everyone, and incorporate the suggestions posted before the end of June.

• How good was the book? What caught your eye?
• Were there parts where you wished for more details?
• Were there confusing parts, problems you did not know how to start, or other roadblocks?
• Have you noticed anything we need to fix about spelling, grammar, and style? Any other comments to the editors?
• What do you think of illustrations?
• Do you feel you could run these activities with kids after reading? If not, what other support would you need?

If you are reading this, you should have received Chapter Two of the Camp Logic book by email. Please answer some of these questions, leave other feedback about Chapter Two, or ask questions. Any feedback will help Mark Saul and Sian Zelbo to improve the book. They will reply to everyone, and incorporate the suggestions posted before the end of June.

• How good was Chapter One overall? What caught your eye?
• Were there parts where you wished for more details?
• Were there confusing parts, problems you did not know how to start, or other roadblocks?
• Have you noticed anything we need to fix about spelling, grammar, and style? Any other comments to the editors?
• What do you think of illustrations?
• Do you feel you could run these activities with kids after reading? If not, what other support would you need

Do you know examples of being immersed in a math culture from the moment the baby was born? How can we make it happen? More details at http://www.moebiusnoodles.com/2014/08/math-like-music/