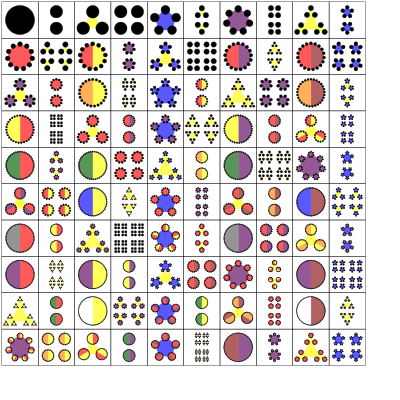
Today your mission is…
Make combination tables and trees, and play guessing games with them.
Ready, Set, Go
Once you build tables and trees, hide parts of them and play guessing games. Or make a puzzle: cut the whole table apart into cells, and put it back together again. In some cases, the same cells can form many different, correct tables!
Option 1. Animal table
Your two variables are heads and bodies. Draw a cat head (or your kid’s favorite animal) in each cell of the first column, and a cat body in each cell of the first row. The corner cell will have the whole cat. Ask the child to pick the next animal. Draw the head of that animal in each cell of the second column, and the body in each cell of the second row.

Option 2. Elements of art and elements of math tables
Make a row or a column with the same color, shape, or visual symbols such as antennae for robots. Print or draw clothes for a table dress-up.

Try systematic changes from cell to cell. For example, keep adding a side to your polygons, or another eye to your monsters.

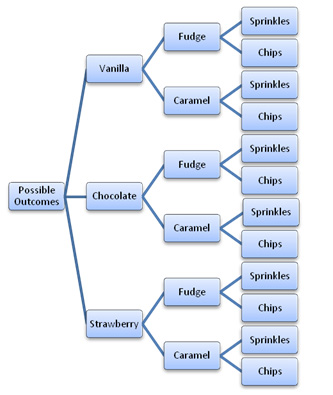
Option 3. More variables: 3D tables and combination trees
Want to use more than two variables? For color-shape-size or any other three variables, build 3D tables. Sticks and styrofoam, or yarn suspended from a cardboard grid takes you to the third dimension. A faster, easier way is to draw combination trees. You might have seen them in sandwich or ice cream shops.
Your forum response
- What multiplication ideas do you see in this topic? How about ideas inspired by algebra?
- Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?
How to help your child to get started
Help kids keep the structure. Bring up famous chimeras and modular constructs from mythology or engineering. Kids may get bored drawing similar pictures in many cells, so help them finish grids quickly. Then play with hiding cells, taking grids apart and other puzzles. Find examples of using grids for combinations in everyday and scientific media.
Ask “How many?” questions about combinations, which lead to multiplication. For example, a grid for three heads and four bodies has twelve chimeras total, because 3x4=12.
Toddlers
Your toddler can place cut-out parts into cells. Some kids get upset if you cut pictures of whole animals into parts, so do that step by yourself, or draw parts separately. Babies who can’t talk yet can point at toys or pictures to help you select the content of the next row or column. Toddlers and young kids often like combinatorics character creation tools in computer games, such as Hero Machine, or combinatorics toys such as Potato Head.
Young children
Kids may want to draw by themselves, or have you draw with their hand in yours. Use
different colors for different rows and columns. Children can “drive” a toy truck along rows and columns, “delivering” parts to each cell. Be prepared: between rows and columns, young children not only change the value of their variables (e.g. red, green, blue for color), but also the type of their variables (e.g. red in the first column, a hat in the second column, triangular shape in the third column). This is fine; just help kids to stay consistent within the same row or column.
Older children
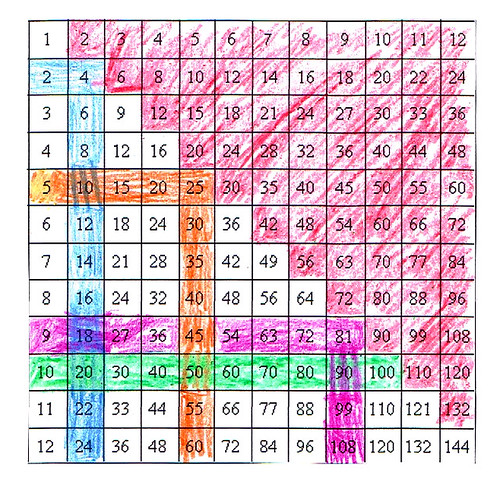
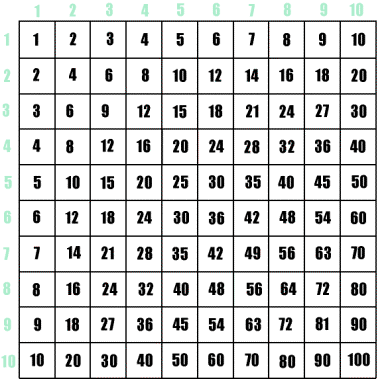
As you read fairy tales or science news, keep an eye on combinations. For example, luminosity and temperature defines different types of stars, such as a red dwarf or a blue giant. Try making number tables, also called structured variation tables. Label columns and rows 1, 2, 3… and come up with your own ways of combining the labels. If you just multiply row and column labels, you will get the familiar times table.
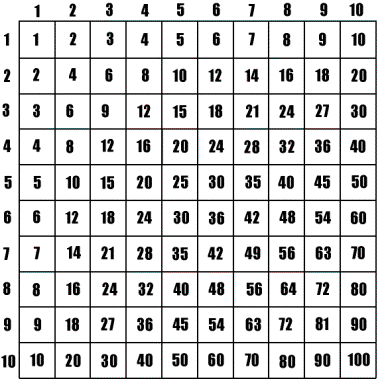
But what if you double the column label and add the row label? Or take the column label to the power of the row label? Or do something else, like the mystery table below? The possibilities for creativity and guessing games are endless! You can make these tables by hand, or program formulas in spreadsheet software.
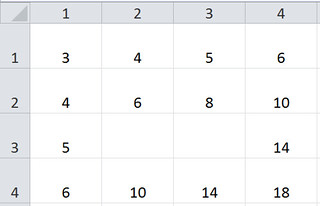
How is this multiplication?
The number of combinations in a table is the number or rows multiplied by the number of columns. In 3D tables, or trees, you multiply the number of values for three or more variables to get the total number of combinations. These visual structures model multiplication even for the youngest kids. Yet we frequently meet adults who have never perceived links between multiplication and combining different pants and shirts, or selecting bread and fillings for sandwiches. It is delightful for kids and adults alike to make this new connection.
Inspired by algebra
Combination tables and trees introduce variables: what varies from row to row, or column to column. Tables prepare kids for coordinate planes. Two tasks, “Find the point with coordinates (2, 3)” and “Find the cell with red square” mean the same algebraic action. The more subtle algebraic idea is covariation, which requires kids to notice two or more variables at once. Whenever you pay attention to both rows and columns, you reason with covariation. Kids use covariation in guessing games with missing cells in tables, or to put a table back together again when it’s cut up into cells.
Frequently Asked Question
My child is simply not interested in multiplication. Whenever I try to bring it up, show him some examples, or explain it to him, he tries to change the subject, finds something else to do, or just doesn’t pay attention. I’ve tried various approaches - living math books, board games, just plain old flash cards, but nothing piques his interest. What can I do? What if he never becomes interested in learning multiplication?
Looks like it’s time for you to move on. Some kids simply dislike some topics, and won’t learn them directly. In such a case, the child will absorb the topic from its connections and applications - if only you keep doing other, interesting mathematics. Math is not linear (even if some curricula are), so it’s very easy to skip a topic for a long while and do something more productive.
Focus on algebraic patterns, explore geometry, get inspired by calculus - there are literally thousands of math topics out there. Print out small times tables with just the results, because the patterns stand out more this way. Put these tables where you do math, for easy reference. Don’t even mention the m-word for a couple of years. Notice how our lists of words that go with activities don’t have multiplication in them…

Words
Variable, combinations, combinatorics, table, tree, covariation
Scavenger hunt
Many cultures have myths about chimeras: creatures combined from animal or human parts, such as pegasus or sphynx. Production companies from car manufacturers to t-shirt makers offer combinations of features. Hunt for words that are made out of other words, such as microphone, telephone, microscope, and telescope. Online memes sometimes feature combination tables or trees, such as alignment charts.

Course links
- All course tasks
- Multiplication Lounge: our open forum for questions, comments, and ideas
- Course participants survey